De berekening van de resonantiefrekwentie van Helmholz resonatoren
vertoont nogal wel verwantschap met die van LC (spoel-kondensator) kringen in
de elektronika. Immers:Dr.Godfried-Willem RAES
Kursus Experimentele Muziek: Boekdeel 4: Organologie, Akoestiek & Experimentele Instrumentenbouw
Hogeschool Gent : Departement Muziek & Drama
| <Terug naar inhoudstafel kursus> |
4300
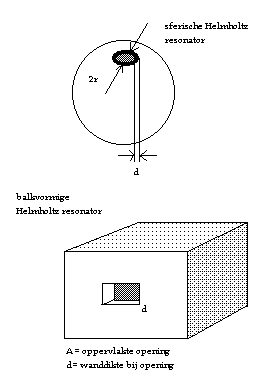
Helmholtz resonatoren
Helmholtz resonatoren vormen de basis van klankkasten zoals toegepast in instrumenten zoals de gitaar, de luit, het klavecimbel, de viool, de mandoline, de harp... Ook in instrumenten uit andere kulturen treffen we ze veelvuldig aan: bamboe resonatoren in de Balinese gender, kallebasresonatoren in de afrikaanse xylofoons, de indiaanse berimbao, de mexikaanse teponatzli... Ook voor blaasinstrumenten worden en werden ze toegepast, zo bvb. in de ocarina, het politiefluitje, de handpalmfluit. Ook kennen we ze als resonator in slaginstrumenten zoals de celesta... Last but not least, vormt ook onze mondholte een Helmholtzresonator, wel eentje met veranderlijk volume en veranderlijke opening. Dankzij deze veranderlijken kunnen we spreken, zingen, fluiten...
Om van een Helmholtz resonator te kunnen spreken, moeten de afmetingen ervan (inhoud en opening van het gat) klein zijn in vergelijking met de golflengte van de resonantiefrekwentie. (memo: l = v / f ) Precies daarom zijn het de resonatoren bij uitstek om aan te wenden wanneer het erop aankomt met een minimum aan ruimtegebruik een zo laag mogelijke toon te versterken (door resonantie) of op te wekken. Het zijn trillingssystemen met slechts een enkele vrijheidsgraad. Precies daarom werden zij tot laat in de 19e eeuw gebruikt voor nauwkeurige frekwentiemetingen in de akoestiek.Noteer dat de aan een kant gesloten buizen die worden gebruikt als resonator in westerse vibrafoons en marimbas geen Helmholtz resonatoren zijn. Hier hebben we immers te maken met trillende luchtkolommen (buizen), die worden berekend zoals gezien in ons hoofdstuk over fluiten en orgelpijpen. Deze buisresonatoren resoneren overigens ook op alle ongeveer even veelvouden (mits eindkorrektie) van de grondfrekwentie. Merk overigens op dat in deze gevallen de fysische lengte van deze resonatoren helemaal niet klein is in verhouding tot de golflengte (het zijn immers halve- of kwartgolf resonatoren), waardoor aan de gestelde voorwaarde voor een Helmholtz resonator alvast niet is voldaan!
De berekening van de resonantiefrekwentie van Helmholz resonatoren
vertoont nogal wel verwantschap met die van LC (spoel-kondensator) kringen in
de elektronika. Immers:
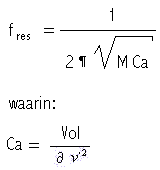
M is het akoestisch equivalent is van de spoel (de inertantie) , en Ca van de kondensator, hier de akoestische kapaciteit.
De vorm van het volume van de Helmholtz resonator heeft geen invloed op de resonantiefrekwentie ervan, wel op de Q-faktor (kwaliteitsfaktor):
(fres= resonantie frekwentie, M= inertantie in g/cm^4 van de opening, ra= akoestische stralingsweerstand)
De scherpste karakteristiek wordt bekomen met zuiver sferische resonatoren. (bollen). Vanzelfsprekend dient het oppervlak aan de binnenzijde van de resonator glad te zijn. De maten van de opening moeten klein zijn in verhouding tot die van de resonator zelf. De inertantie kan voor resonatoren met een ronde opening worden berekend op grond van de fysische afmetingen van de resonator volgens de hierboven reeds gegeven formule:
(sigma = densiteit van lucht in g/cm^3, r= straal van de opening in cm, d= wanddikte bij de opening in cm. De kontante faktor 1.7 in de formule komt overeen met de vierkantswortel uit Pi en geldt dan ook alleen voor ronde openingen.)
(v= geluidssnelheid in cm/s)
De kwaliteitsfaktor wordt dan na subsitutie:
en
deze waarde dienen we zo groot mogelijk (zeker > 1) te maken, tenminste wanneer
een duidelijke resonantie wenselijk is. Dat is overigens niet steeds het geval:
immers wanneer we een klankkast voor een instrument maken, willen we meestal
niet een klankkast bekomen die slechts voor een enkele toonhoogte goed (lees
luid) klinkt.
Voor niet cirkelvormige openingen moet de formule gewijzigd worden in:
, waarin Opp dan staat voor de oppervlakte van de opening.
Overigens gelden hier precies dezelfde wetten en wetmatigheden als die welke
we hebben ontmoet in ons boekdeel over elektronika (boekdeel 2) in verband met
spoelen, kondensatoren en weerstanden. Vanuit elektronisch opzicht is een Helmholtz
resonator dan het akoestische equivalent van een weerstand-spoel-kondensator
serieschakeling.
De akoestische kapaciteit wordt gegeven door:
Merk op dat die uitsluitend een funktie is van de inhoud van de resonator en niet van de vorm of de opening. De inertantie (M) is het akoestisch equivalent van de induktie (spoel) in de elektronika. De formule voor M in het algemene geval (dus niet alleen voor ronde openingen) ziet eruit als:
Berekening van de resonantiefrekwentie:
Voor resonatoren met een ronde opening:
,
of in Basic komputer notatie:
f = (r * v) / ((2* Pi) * SQR( Vol * (d + ( 1.7 * r ))))
v = geluidssnelheid in cm/s
f = frekwentie van de resonator in Hz
d = wanddikte aan de opening in cm
r = straal van de opening, in cm
Vol = volume van de resonator, in cm^3 of cc
eenheden: cm, cc, s
Voor resonatoren met een willekeurige opening krijgen we:
, of in Basic notatie:
f = ( v / (2 * Pi)) * SQR[ A / ( Vol * ( d + SQR( A )))]
waarin dan:
A = oppervlakte van de opening in vierkante centimeter
Nota: wanneer we meerdere gaten hebben, moeten de oppervlaktes daarvan opgeteld worden. Dit geval doet zich bvb. voor wanneer we de kastresonantie willen berekenen van strijkinstrumenten uit de vioolfamilie, die immers van twee f-gaten zijn voorzien. Ook bij chinese temple blocks is dit het geval trouwens.
Berekening van het volume:
Voor resonatoren met een ronde opening:
Vol = ((r^2) * (v^2)) / (4 * Pi * (f^2)* (d + (1.7*r)))
Voor resonatoren met een willekeurige opening:
Vol = ( A * (v^2)) / (4 * (Pi^2) * (f^2)* (d + SQR(A)) )
of klassiek geschreven:
Berekening wanddikte:
Voor resonatoren met een ronde opening:
d = ( (( r^2 )*( v^2 )) / (4 * Pi* Vol * (f^2)) ) - (1.7 * r)
merk op dat de konditie geldt dat:
1.7 * r <= (r^2)*(v^2) / (4*Pi*Vol*(f^2))
Voor resonatoren met een willekeurige opening:
d = [((v^2) * A) / (4 * (Pi^2) * (f^2) * Vol)] - SQR(A)
merk op dat de konditie geldt dat:
SQR(A) <= A*(v^2) / (4*(Pi^2)*Vol*(f^2))
Berekening van de opening:
Voor resonatoren met een ronde opening:
Hiervoor lossen we de kwadraatvergelijking in r op:
[(c^2)/ (4*Pi * Vol * (f^2))]* (r^2) - [1.7]*r - d = 0
we stellen:
en berekenen de diskriminant:
D = (b'^2) - 4*a'*c'
Aangezien a' positief is en c' negatief, zal de tweede wortel van deze vergelijking ook de grootste zijn, dus:
r = (- b' + SQR(D)) / (2* a')
waarmee we, na substitutie van a, b en D gemakkelijk r kunnen berenenen. Wanneer D negatief zou zijn, zijn er geen reele wortels en is de resonator fysisch onmogelijk.
Voor resonatoren met een willekeurige opening:
Hiervoor lossen we de verkapte kwadraatvergelijking in A op:
[(c^2)/ (4*(Pi^2) * Vol * (f^2))]* A - SQR(A)- d = 0
eerst herleiden we dit , door substitutie van P = SQR(A) tot een vierkantsvergelijking in P:
[(c^2)/ (4*(Pi^2) * Vol * (f^2))]* (P^2) - P - d = 0
waarna we weer stellen:
en berekenen de diskriminant:
D = (b'^2) - 4*a'*c'
Aangezien a' positief is en c' negatief, zal de tweede wortel van deze vergelijking ook de grootste zijn, dus:
r = (- b' + SQR(D)) / (2* a')
waarmee we, na substitutie van a, b en D gemakkelijk r kunnen berekenen. Wanneer D negatief zou zijn, zijn er geen reele wortels en is de resonator fysisch onmogelijk. De gezochte oplossing is , aangezien we stelden P = SQR(A)
A = [(- b' + SQR(D)) / (2* a')]^2
Om de praktische berekeningen gemakkelijk te kunnen uitvoeren schreven we een klein programma in PowerBasic (Console Compiler).
Dit is, zoals ook andere utilities voor akoestische berekeningen aan te treffen op onze website onder een speciaal directory: ../akoestiek/...
Noteer dat deze software alleen loopt op PC's, maar dan wel onder alle Windows versies evenals onder DOS!
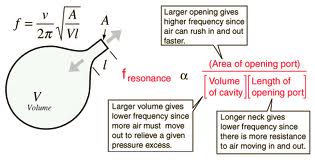
De praktische uitvoering van een Helmholtz resonator kan worden gedaan met een naar binnen gebrachte 'schoorsteen', zoals in volgende afbeelding:
Het is duidelijk dat voor een aantal praktische toepassen dit een ruimtebesparing met zich kan brengen. Enkele andere berekeningswijzen en vormgevingen:
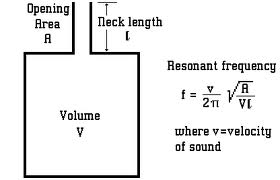
Praktische toepassingen in de organologie en de instrumentenbouw
Opmetingen van de fysische maten
1.- De gitaar:
Hier hebben we te maken met een Helmholtz resonator met een ronde opening. De oppervlakte daarvan is uiteraard gemakkelijk te berekenen. De inhoud evenwel is heel wat moeilijker te bepalen. De eenvoudigste metode bestaat erin het instrument volledig te vullen met een droog fijnkorrelig materiaal (piepschuimbolletjes, rijst, tapioca of iets dergelijks). Daarna wordt de klankkast weer leeggemaakt in een recipient en vervolgens kan met een meetbeker, het volume eenvoudig afgelezen worden.
2.- De viool-familie
Het volume van deze instrumenten kan worden bepaald zoals hiervoor uitgelegd in verband met de gitaar. (Voor de cello en a fortiori de kontrabas gebruiken we best piepschuimkorrels zoals gebruikt als vulling voor beanbags of zitzakken). De bepaling van de oppervlakte van de f-gaten langs wiskundige weg is erg moeilijk. Maar ook hier kunnen we een empirische truuk gebruiken: teken de f-gaten heel precies af of een stuk tekenpapier. (Aandrukken en kalkeren met de achterkant van een potlood werkt erg goed). Dan knippen we deze vorm zo exakt mogelijk uit een materiaal waarvan we het soortelijk gewicht en de dikte kennen of makkelijk kunnen te weten komen. Tenslotte wegen we de in dat materiaal uitgeknipte f-gaten op een nauwkeurige weegschaal (apotekersbalans of desnoods een briefweger bvb.).
Meting van de resonantie frekwentie
Hiervoor moeten we beschikken over een toongenerator, een transducer en een voldoende grote hoeveelheid zwaar dempingsmateriaal (droog fijn zand bvb.). Het instrument wordt zoveel mogelijk bedolven onder het dempingsmateriaal teneinde de trillingen van met materiaal waaruit de klankkast is gebouwd zoveel mogelijk te verhinderen. Voor een minder precieze meting volstaat het vaak met de vlakke hand het bovenblad van het instrument zo goed mogelijk te dempen, terwijl je het instrument op de blote dijen aangedrukt houdt. Door dit laatste wordt ook het onderblad redelijk gedempt. Bij gitaren is het voor een precieze meting soms eenvoudiger het vlakke bovenblad in te klemmen tussen een dikke stapel kranten. Vervolgens wordt de transducer in de klankkast gebracht. Voor dit doel is een van de speakertjes van een walkman of MP3-speler koptelefoontje van goede kwaliteit geschikt. De voorkeur gaat uit naar een redelijk hoogohmig exemplaar (32 Ohm of meer). Dan wordt, beginnend bij 20Hz de toongenerator ingeschakeld en luisteren we naar het optreden van de eerste uitgesproken resonantietoon. De frekwentie waarbij de luidheid daarvan een maximum vertoont, is de resonantiefrekwentie van de klankkast van het instrument. Bij goede instrumenten mag deze resonantietoon niet te scherp afgetekend zijn, maar moet hij over een gebied van toch wel minstens een terts uitgesmeerd optreden. In de akoestiek noemt men dit de Q-faktor van de resonator (kwaliteitsfaktor). Hoe groter die is, hoe unieker en piekvormiger de resonantiekurve.
Enkele in de praktijk opgemeten waarden van klankkasten die zich minstens voor een relevant deel gedragen als Helmholtz resonatoren::
sopraangitaar:
Altviool:
Cello:
Pochette:
Mandoline:
Viool (1/2, studieviool)
Helmholtz resonatoren treffen we ook veelvuldig aan in talloze etnische muziekinstrumenten: de afrikaanse marimba's zijn voorzien van gedroogde kalebassen met een gat, als Helmholtz resonator gestemd op de grondtoon van de boven het gat aangebrachte klankstaaf. Ook ocarina's zijn akoestisch gezien Helmholtz resonatoren.
Een historische noot:
In de 19e eeuw, en zelfs nog tot vrij laat in de eerste helft van de 20e eeuw, waren Helmholtz resonatoren de enige meetinstrumenten waarover fysici die zich met akoestisch onderzoek bezighielden konden beschikken om het spektrum van geluiden te onderzoeken. Zij beschikten daarvoor over een onvoorstelbaar groot aantal dergelijke resonatoren, veelal gemaakt uit geblazen glas, zodat ook smalle bandjes uit een spektrum konden worden onderzocht. Omdat zij er evenwel van uitgingen dat boventonen zich wel zouden gedragen als gehele veelvouden van een gegeven grondtoon en zij hun resonatoren dan ook bij voorbaat zo stemden, werd veel van hun 'harmonische teorie' op die wijze verkeerdelijk aan de werkelijkheid opgedrongen.
De afbeeldingen hieronder tonen dergelijke resonatoren zoals vroeger gebruikt in akoestisch onderzoek:
Filedate: 980810 - Last update: 2013-02-27
| Terug naar inhoudstafel akoestiek kursus: <Index Kursus> | Naar homepage dr.Godfried-Willem RAES | Run Helmholtz-resonator program |
