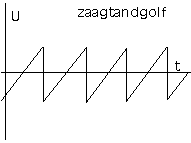 De
spektrale samenstelling nu, blijkt duidelijk uit de weergave in het frekwentiedomein:
De
spektrale samenstelling nu, blijkt duidelijk uit de weergave in het frekwentiedomein:Dr.Godfried-Willem RAES
Kursus Experimentele Muziek: Boekdeel 2: Interaktieve systemen en live electronics
Hogeschool Gent - School of Arts
|
Klankonderzoek 1982-2014 ARCHIVAL |
2000: Inleiding:
Voor het opdoen van de nodige praktische ervaring in dit gedeelte van de kursus zullen de studenten dienen te kunnen beschikken over volgende toestellen en uitrusting:
Aangezien dergelijke uitrusting niet behoort tot het arsenaal spullen die in een konservatorium in traditionele zin thuishoren en omdat ze voor de hier behandelde materie onontbeerlijk zijn, heb ik zelf een basisuitrusting in de klas onderdak doen vinden ten behoeve van de studenten. Ook voor dit deel van de kursus zal het beschikken over een komputer (geen MAC!) snel onontbeerlijk blijken. Een wetenschappelijke zakrekenmachine is ook erg handig...
Algemene Begrippen uit de elektriciteit
Hoewel alle hier volgende begrippen uit de elektriciteit bekend dienen te zijn aan wie Hoger Middelbaar Onderwijs met sukses beeindigd heeft, lijkt het nuttig ze hier toch even in herinnering te brengen. De studenten die dit alles wat erg ver in het geheugen zitten hebben, weten zo ook meteen wat ze dan maar beter nog eens kunnen opzoeken in hun diverse handboeken voor wiskunde en fysika, of -meer specifiek gericht op deze paragrafen en hun verwerking, in een goed elektronikaboek. De lektuur van Horowitz-Hill 'Elektronika, Kunst & Kunde' in 2 boekdelen recent ook verschenen in het nederlands nij de uitgeverij Elektuur, raad ik van harte aan. Overigens zijn in de bibliografie aan het eind van deze syllabus, naast dit werkelijk uistekende boek, heel wat goede naslagwerken opgenomen.
Wie een meer diepgaande baziskennis wil opfrissen of verwerven m.b.t. de meer wiskundige behandeling van de passieve komponenten in de elektronika, kan o.m. terecht in Thomas L. Floyd 'Electronic circuits: electron-flow version'.
Primaire parameters:
Dit zijn de fundamentele fysische grootheden waarmee we in verband met elektriciteit en elektronika te maken krijgen en waarvan andere gebruikelijke grootheden afgeleid kunnen worden.
parameter eenheid symbool
|
Spanning |
Volt [V] |
U |
|
Stroom |
Ampere [A] |
I |
|
Tijd |
sekonde [s] |
t |
|
Faze (hoek) |
graad (°) |
Phi (j) |
De fazehoek kan ook worden uitgedrukt in radialen (2Pi=360graden).
Zonder gebruik te maken van enige fysische wet, kunnen we hieruit reeds volgende vaak gebruikte parameters afleiden:
|
Frekwentie |
Herz [Hz] |
f |
frekwentie is een maat voor het aantal keer dat een periodiek verschijnsel zich voordoet per tijdseenheid (in dit geval steeds de sekonde). ( 1/s = Hz = frekwentie). In plaats van Hz kan je ook als eenheid de exponentiele notatie s-1 gebruiken. Wie vaak met komputers werkt zal de notatie ^-1 allicht handig vinden. De periode, de tijd van een enkel verschijnsel uit een periodieke reeks wordt steeds uitgedrukt in sekonden en voorgesteld door het symbool T.(steeds als hoofdletter, om het onderscheid te maken met t voor de tijd in de algemeenste zin).
Eveneens langs zuiver wiskundige weg kunnen we periodieke verschijnselen ook kenmerken en meten in termen van omtreksnelheid, hoeksnelheid of cirkelfrekwentie:
|
Omtreksnelheid |
w=2*p*f |
Merk op dat hier griekse letters worden gebruikt: pi en kleine omega.
Secondaire parameters:
Alle sekondaire parameters kunnen op grond van bewezen fysische wetten uit de primaire worden afgeleid. De als sekondaire parameters geintroduceerde eenheden zijn niet strikt nodig, maar vereenvoudigen wel de uitdrukkingen in formules aanzienlijk. Bovendien zijn zij gesteund op de meest fundamentele wetten van de elektriciteit, en is de grondige kennis ervan meteen ook een garantie voor een goed inzicht in deze wetten.
|
- Weerstand |
Ohm ( W) |
R |
|
|
Wet van Ohm : |
U = I * R |
||
|
- Wisselspanning |
sinus |
Volt (V) |
U = Up*sin(j) |
|
- Impedantie |
Ohm (W) |
Z |
|
|
van een weerstand : |
Z = R |
||
|
van een spoel: |
Z = 2*p¦*L |
||
|
van een kondensator: |
Z = 1/(2*p*¦*C) |
||
|
- Vermogen |
Watt |
P |
|
|
D.C.: |
P = U*I |
||
|
A.C.: (sinus) |
P = U*I* cos(j) |
||
|
- Lading |
Coulomb |
Q |
|
|
- Kapaciteit |
Farad |
C |
|
|
- Induktie |
Henry |
L |
|
|
- Konduktiviteit |
mho |
( = 1/R ) R-1 |
|
|
- Arbeid |
Joule - Wh |
A |
Leer deze eenheden, formules en samenhangen goed uit het hoofd. Je zult ze -ook buiten deze kursus- vaak handig kunnen gebruiken!
De decibell, een relatieve eenheid waarmee verhoudingen van grootheden van allerlei aard (spanningsverhoudingen, vermogens, signaal/ruis, stromen...) kunnen worden uitgedrukt, behandelen we niet hier, hoewel we er doorheen dit boekdeel wel degelijk mee te maken zullen krijgen. Voor een beknopte uiteenzetting terzake verwijzen we naar ons hoofdstuk over audiotechnologie.
Domeinen:
Elektronische schakelingen -net zoals muziek zelf trouwens- kunnen vanuit twee verschillende fysische gezichtpunten worden beschouwd, berekend en geanalyseerd:
In het tijdsdomein worden alle signalen bekeken als het verloop van een parameter (bvb. Spanning of stroom...) in de tijd. Zo geeft de funktie
U = Umax * sin (2*Pi* 440. T)
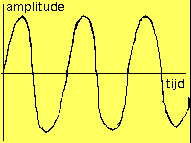
ons het verloop van de momentane waarde van een wisselspanning met frekwentie 440Hz en een maximale amplitude van Umax in de tijd. Een muzikale la dus. De ‘horizontale’ as in bij deze beschouwing dus steeds het lineaire tijdsverloop. Dit is de grafische voorstelling zoals we die te zien krijgen op het beeldscherm van een oscilloskoop.
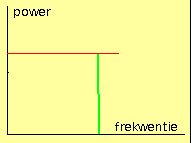
Komplexe signalen -zoals onder andere het elektrische equivalent van muziek er een is- kunnen inzichtelijker worden behandeld vanuit een perspektief waarbij we horizontaal de frekwentie (toonhoogte) uitzetten tegen een andere parameter op de vertikale as. Voor een enkelvoudige sinus ziet de grafiek er dan heel eenvoudig uit als een enkel vertikaal lijntje op een horizontale frekwentieas. De hoogte van het lijntje (de spektraalkomponent) komt overeen met de energie in de betreffende frekwentieband.
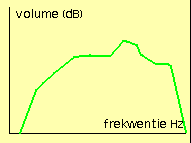
De frekwentiekarakteristiek van een versterkerschakeling, van een koncertzaal, van een muziekinstrument evenals de spektrale samenstelling van een klank kunnen zo heel wat inzichtelijker worden uitgedrukt. Een frekwentie-karakteristiek kan er bvb. uitzien zoals op de grafiek hierbij. (de horizontale as is de frekwentie, de vertikale de intensiteit)
Willen we beide domeinen gelijktig weergeven, dan moeten we beroep doen op driedimensionele grafieken. Dit blijkt bvb. nodig wanneer we een beeld willen krijgen van het verloop van een spektrum in de tijd.
Nog een voorbeeld: Een zaagtandsignaal bevat alle boventonen in aflopende sterkteverhoudingen. In het tijdsdomein -zo krijgen we het te zien op een oscilloskoop- zie het eruit als:
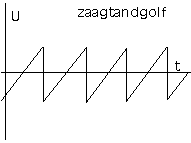 De
spektrale samenstelling nu, blijkt duidelijk uit de weergave in het frekwentiedomein:
De
spektrale samenstelling nu, blijkt duidelijk uit de weergave in het frekwentiedomein:
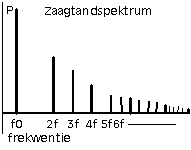
Hierna volgt een beknopte voorstelling van de diverse in de elektronika gebruikelijke komponenten, hun schematische voorstelling, hun eenheden en grootheden.
Passieve Komponenten:
a.elementaire
- Draad of verbinding
relevante eenheden en grootheden: lengte, weerstand per meter, stroom, materiaal, isolatie
- Weerstand
relevante eenheden en grootheden: R , P , Umax
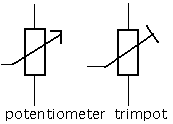
varianten worden gevormd door de regelbare weerstanden: potentiometers, met lineaire of logaritmische karakteristiek, schuiftypes of draaitypes, multiturn, trimpotmeters...
Vergeet ook niet dat zowat het gros van de meest voorkomende elektrische toestellen eigenlijk weerstanden zijn. Zo bijvoorbeeld de lamp, een weerstand met een stroomafhankelijke weerstandskarakteristiek, iets wat ook in de elektronika omwille van die eigenschap vaak gebruikt wordt.
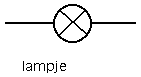
- Kondensator
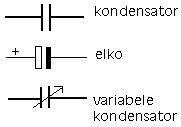 relevante eenheden en grootheden: C
, Umax
relevante eenheden en grootheden: C
, Umax
Formules:
impedantie van een kondensator bij een frekwentie f:
Xc = 1 / 2*Pi*f*C
momentane spanning over een kondensator:
v = Vf + (Vi - Vf)* e^(-t/T)
Vf= eindspanning
Vi= beginspanning
e = grondgetal natuurlijke logaritmen
T = RC produkt (ladingsweerstand * cap.)
t = tijdsinterval
Na een tijdsinterval van 5*R*C heeft de kondensator zijn eindwaarde binnen 1% bereikt.Wanneer de kondensator volledig is ontladen bij het begin van het ladingsproces kan de formule vereenvoudigd worden tot:
v = Vf ( 1 - e^(-t/RC))
Tussen stroom en spanning bestaat een fazeverschil van -90 graden (Pi/2). Gebruik makend van komplexe getallen, wordt de impedantie van een kondensator bij een gegeven frekwentie dan
Zc = 0 -j*Xc , of, in poolkoordinaten:
Zc= Xc <-Pi/2
Spoel
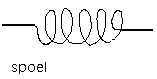

relevante eenheden en grootheden: L , Imax, R, Qfaktor
Formules:
De formules voor spoelen vormen het komplement van die voor kondensatoren:
impedantie (reaktantie) van een spoel bij een frekwentie f:
Xl = 2*Pi*f*L
Gebruik makend van komplexe getallen, en rekening houdend met de door een spoel veroorzaakte fazeverschuiving van 90graden (Pi/2), wordt de impedantie van een spoel bij een gegeven frekwentie dan Zl = 0 + j*Xl, of, in poolkoordinaten: Zl= Xl <Pi/2
Formules voor de samenstellingen van weerstanden, kondensatoren en spoelen:
Doordat bij schakelingen met capacitieve en reaktieve komponenten onvermijdelijk fazeverschuivingen tussen stroom en spanning zullen optreden, dienen we daarmee terdege rekening te houden. Het is in de elektronika gebruikelijk daartoe gebruik te maken van hetzij polaire koordinaten (een getallenkoppel bestaande uit een impedantie enerzijds en een hoek (faze) anderzijds) hetzij van het komplexe getallenstelsel uit de wiskunde waarbij een komplex getal wordt opgebouwd uit een reeel deel en een imaginair deel. Beide voorstellingswijzen zijn equivalent en in elkaar omzetbaar. Polaire koordinaten lenen zich echter beter tot het uitvoeren van vermenigvuldigingen en delingen, terwijl komplexe getallen eenvoudig zijn af te trekken en op te tellen.
We brengen de omzettingsregels even in herinnering:
|
komplexe getallen |
naar |
polaire voorstelling: |
|
a + j* b |
= |
SQR((a^2) + (b^2)), ATN(b/a) |
|
reeel deel + imaginair deel |
numerieke waarde, hoek |
|
poolkoordinaten |
naar |
komplexe getallen |
|
C, Phi |
= |
C*cos(Phi) + j*C*sin(Phi) |
|
numerieke waarde, hoek |
reeel deel + imaginair deel |
Het imaginaire getal i uit de wiskunde wordt in de elektronika steeds met de letter j voorgesteld, vanwege het feit dat i reeds langer in gebruik was als simbool voor de voorstelling van een stroom.
( j = SQR(-1) )
Optelling en aftrekking van komplexe getallen:
(A + j.B) + (C + j.D) = (A+B) + j(C + D)
(A + j.B) - (C + j.D) = (A - B) + j( C - D)
Vermenigvuldiging en deling in poolkoordinaten:
(N, PhiN) * (M, PhiM) = (N*M , PhiN + PhiM)
(N, PhiN) / (M, PhiM) = (N/M, PhiN - PhiM)
Serieschakelingen:
Z = R - j*Xc of Z = SQR(R^2 + Xc^2), -ATN(Xc/R)
Z = R + j*Xl of Z = SQR(R^2 + Xl^2), ATN(Xl/R)
Z = R + j*Xl - j*Xc of Z = SQR(R^2 + (Xl-Xc)^2), ATN((Xl-Xc)/R)
Wanneer we gebruik maken van komplexe getallen geldt de algemene regel dat bij serieschakeling van willekeurige onderdelen , de komplexe impedantie van het totaal steeds gelijk is aan de komplexe som van alle komplexe impedanties der onderdelen.
Parallelschakelingen:
Deze zijn eenvoudiger te berekeningen onder gebruikmaking van poolkoordinaten (vektoren) en wel alsvolgt:
Z = (R * Xc) / SQR((R^2) + (Xc^2)), (-90 + ATN (Xc/R))
Z = (R * Xl) / SQR((R^2) + (Xl^2)), (90 - ATN (Xl/R))
3. Weerstand + kondensator + spoel:
Z = 1 / SQR((1/R^2) + (1/Xc-1/Zl)^2), ATN((Xl-Xc)/R)
![]()
Deze formules hoeven we overigens helemaal niet uit het hoofd te leren. Het enige wat we wel moeten weten is dat bij serieschakeling de vervangingsimpedantie wordt berekend door de optelling (algebraisch en gebruik makend van het komplexe getallenstelsel) van de impedanties der komponenten:
Ztot = Z1 + Z2 + Z3 + ...
terwijl voor de parallelschakeling de inverse vervangingsimpedantie wordt berekend door optelling van de inverse impedanties der komponenten, dus:
1/ Ztot = (1/Z1) + (1/Z2) + (1/Z3) + ...
Om het rekenwerk met komplexe getallen voor de studenten te vergemakkelijken, schreven we een klein basic programma -kompileerbaar tot library- waarin alle algebraische bewerkingen op komplexe getallen zowel cartesisch als in poolkoordinaten als procedures zijn opgenomen. De enige programmeertaal die dergelijke wiskundige funkties als standaard kent, is helaas Fortran... Het bestuderen van de bronkode van dit programma is erg leerzaam voor wie niet (meer) goed vertrouwd is met de algebra van het middelbaar onderwijs. Bovendien zijn alle hiervoor gegeven formules erin opgenomen, en kan het dus als ‘repertorium’ gebruikt worden.
Sedert 1998 zijn alle funkties voor komplexe rekenkunde een vast deel van de GMT programmeertaal door mij ontwikkeld voor real time algoritmische kompositie. Aangezien ze werden opgenomen in een DLL kunnen ze met eender welke programmeertaal worden gebruikt. (cfr. g_indep.dll).
<Naar verdere elektronische onderdelen>
' include file with declarations for the complex math library: COMPMATH.BI
Een recentere versie van de hieronder weergeven kode vormt deel uit van onze <GMT> programmeertaal en is terug te vinden in de library g_indep.dll.
TYPE Complex
real AS DOUBLE
imag AS DOUBLE
END TYPE
TYPE Polar
mag AS DOUBLE
ang AS DOUBLE
END TYPE
CONST Pi = 3.141592653589#
CONST Pi2 = Pi * 2#
CONST Pih = Pi / 2#
CONST Infinite = 1D+66
CONST Zero = 1D-66
' procedures
' konversie van polair naar cartesisch en vice versa:
DECLARE SUB P2C (P AS Polar, C AS Complex)
DECLARE SUB C2P (C AS Complex, P AS Polar)
' konversie van Rad naar graden en vice versa:
DECLARE FUNCTION Rad2Deg# (rad#)
DECLARE FUNCTION Deg2Rad# (degrees#)
' algebraische
funkties op poolkoordinaten:
DECLARE SUB MulPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
DECLARE SUB DivPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
DECLARE SUB AddPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
DECLARE SUB SubPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
DECLARE SUB InvPol (G1 AS Polar, Gr AS Polar)
DECLARE SUB ConPol (G1 AS Polar, Gr AS Polar)
DECLARE SUB ParPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
' algebraische funkties met cartesische komplexe getallen
DECLARE SUB MulCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DECLARE SUB DivCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DECLARE SUB AddCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DECLARE SUB SubCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DECLARE SUB InvCom (G1 AS Complex, Gr AS Complex)
DECLARE SUB ConCom (G1 AS Complex, Gr AS Complex)
DECLARE SUB ParCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DECLARE FUNCTION MagCom# (G1 AS Complex)
DECLARE FUNCTION AngCom# (G1 AS Complex)
' elektronische funkties en procedures:
DECLARE FUNCTION OmegF# (f#)
DECLARE SUB XcCar (C#, f#, G AS Complex)
DECLARE SUB XcPol (C#, f#, G AS Polar)
DECLARE SUB XlCar (L#, f#, G AS Complex)
DECLARE SUB XlPol (L#, f#, G AS Polar)
En hier volgt de eigenlijke programmamodule:
' ***************************************************
' * Hogeschool Gent - Departement Muziek en Drama *
' * Laboratory for Experimental Musics *
' * COMPMATH.BAS *
' * dr.Godfried-Willem RAES *
' ***************************************************
' Basic complex math support: Cartesian and Polar complex numbers
' 23.05.1997: Debugged and tested
' 15.06.1997: extended with functions for serial & parallel circuits compiled
to library
' 17.06.1997: extended with basic electronic functions . works as QLB
REM $INCLUDE: 'COMPMATH.BI'
SUB AddCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
Gr.real = G1.real + G2.real :Gr.imag = G1.imag + G2.imag
END SUB
SUB AddPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
' eerst omzetten naar complex
cartesisch
DIM C1 AS Complex
DIM C2 AS Complex
DIM Cr AS Complex
P2C G1, C1
P2C G2, C2
AddCom C1, C2, Cr
C2P Cr, Gr
END SUB
FUNCTION AngCom# (C AS Complex) '
this functions returns the phase angle in Rad for a complex number
IF C.real <> 0 THEN
ang# = ATN(C.imag / C.real)
ELSE
ang# = SGN(C.imag) * Pi / 2#
END IF
' correction for quadrant-sign: 0-180 gr & 0-> -180gr
IF C.real < 0 THEN ang# = Pi + ang#
IF ang# > Pi THEN ang# = -Pi2 + ang#
AngCom# = ang#
END FUNCTION
SUB C2P (C AS Complex, P AS Polar) '
converts cartesian complex numbers to polar coordinates
P.mag = MagCom#(C)
P.ang = AngCom#(C)
END SUB
SUB ConCom (G1 AS Complex, G2 AS Complex) '
returns the conjugate (komplex toegevoegd getal) number
G2.real = G1.real
G2.imag = -G1.imag
END SUB
SUB ConPol (P1 AS Polar, P2 AS Polar) '
complex conjugate in polar form
DIM G1 AS Complex, G2 AS Complex
P2C P1, G1
ConCom G1, G2
C2P G2, P2
END SUB
FUNCTION Deg2Rad# (degrees#)
Deg2Rad# = degrees# * Pi / 180#
END FUNCTION
SUB DivCom (G1 AS Complex, G2 AS Complex, Gr AS
Complex) ' eerst omzetten
naar polair:
DIM P1 AS Polar, P2 AS Polar, Pr AS Polar
C2P G1, P1
C2P G2, P2
DivPol P1, P2, Pr
P2C Pr, Gr
END SUB
SUB DivPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
Gr.mag = G1.mag / G2.mag
Gr.ang = G1.ang - G2.ang
END SUB
SUB InvCom (G1 AS Complex, Gr AS Complex) '
calculates 1/G1
DIM P1 AS Polar
DIM P2 AS Polar
P2.mag = 1#
P2.ang = 0
DIM Pr AS Polar
C2P G1, P1
DivPol P2, P1, Pr
P2C Pr, Gr
END SUB
SUB InvPol (G1 AS Polar, Gr AS Polar) '
calculates 1/G1
IF G1.mag <> 0 THEN
Gr.mag = 1# / G1.mag
ELSE
Gr.mag = 1D+66
END IF
Gr.ang = -G1.ang
END SUB
FUNCTION MagCom# (C AS Complex)
' returns the magnitude or modulus of a complex number.
' This is the first part of the same number in polar form
MagCom# = SQR((C.real ^ 2#) + (C.imag ^ 2#))
END FUNCTION
SUB MulCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
DIM P1 AS Polar
DIM P2 AS Polar
DIM Pr AS Polar
C2P G1, P1
C2P G2, P2
MulPol P1, P2, Pr
P2C Pr, Gr
END SUB
SUB MulPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
Gr.mag = G1.mag * G2.mag
Gr.ang = G1.ang + G2.ang
END SUB
FUNCTION OmegF# (f#) '
cirkelfrekwentie
OmegF# = Pi2 * f#
END FUNCTION
SUB P2C (P AS Polar, C AS Complex)
C.real = P.mag * COS(P.ang)
C.imag = P.mag * SIN(P.ang)
END SUB
SUB ParCom (G1 AS Complex, G2 AS Complex, G3 AS
Complex) ' 1/Z = 1/Z1 + 1/Z2
==> Z = (Z1*Z2)/(Z1+Z2)
DIM PsumC AS Complex, PsumP AS Polar, Pprod AS Polar, G1pol AS Polar, G2pol
AS Polar, G3pol AS Polar
AddCom G1, G2, PsumC
C2P PsumC, PsumP: ' convert to polar
C2P G1, G1pol
C2P G2, G2pol
MulPol G1pol, G2pol, Pprod
DivPol Pprod, PsumP, G3pol
P2C G3pol, G3
END SUB
SUB ParPol (G1 AS Polar, G2 AS Polar, G3 AS Polar)
' 1/Z = 1/Z1 + 1/Z2 ==> Z = (Z1*Z2)/(Z1+Z2)
DIM Psum AS Polar, Pprod AS Polar
AddPol G1, G2, Psum
MulPol G1, G2, Pprod
DivPol Pprod, Psum, G3
END SUB
FUNCTION Rad2Deg# (rad#)
Rad2Deg# = rad# * 180# / Pi
END FUNCTION
SUB SubCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
Gr.real = G1.real - G2.real
Gr.imag = G1.imag - G2.imag
END SUB
SUB SubPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)
' omzetten naar complex cartesisch
DIM C1 AS Complex, C2 AS Complex, Cr AS Complex
P2C G1, C1
P2C G2, C2
SubCom C1, C2, Cr
C2P Cr, Gr
END SUB
SUB XcCar (C#, f#, Gr AS Complex)
Gr.real = 0
IF C# * f# > 0 THEN
Gr.imag = -1# / (OmegF#(f#) * C#)
ELSE
Gr.imag = -Infinite
END IF
END SUB
SUB XcPol (C#, f#, Gr AS Polar)
IF f# * C# > 0 THEN
Gr.mag = 1# / (OmegF#(f#) * C#)
ELSE
Gr.mag = Infinite
END IF
Gr.ang = -Pih
END SUB
SUB XlCar (L#, f#, Gr AS Complex)
Gr.real = 0
Gr.imag = OmegF#(f#) * L#
END SUB
SUB XlPol (L#, f#, Gr AS Polar)
Gr.mag = OmegF#(f#) * L#
Gr.ang = Pih
END SUB
Dit programma is ter beschikking van de studenten op de klaskomputers in volgende vormen:
COMPMATH.BAS bronkode
COMPMATH.BI deklaraties en konstanten
COMPMATH.QLB library voor gebruik in de interpreter
COMPMATH.LIB library voor kompilatie
Evenals op internet op: ../mathlib/compmat.bas
b.komplexe onderdelen
-Kristal
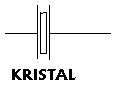
relevante eenheden en grootheden: fres, Umax
verdere eigenschappen: bandbreedte, temperatuurcoefficient
- Keramisch Filter
relevante grootheden: fres, Umax
Demping, Q faktor
- Delay line
relevante eenheden en grootheden: t, Imax
-Luidspreker
(Zie boekdeel over audiotechnologie voor een uitvoerige behandeling)
P, Z, fmin, fmax, efficientie (dB)
- Mikrofoon (Zie boekdeel over audiotechnologie)
U, gevoeligheid (dB), fmin, fmax
maximale geluidsdruk
S/R signaal ruisverhouding
- Antenne
relevante grootheden: Gain (dB), Frekwentie, Bandbreedte
Vorm: spriet , draad of dipool
- Transformator
relevante grootheden: primaire spanning, sekundaire spanning, transformatieverhouding, impedantie
vermogen, stroom, frekwentie, strooiveld, efficientie
a. elementaire
1. halfgeleiders
- halfgeleiderdiodes, siliciumdiode, germaniumdiode
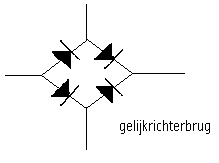
- Graetz-brug of gelijkrichterbrug
- Zenerdiode, Gunn Diode, GaAs-diode & LED, Seleniumdiode, varicapdiode
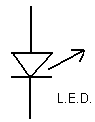
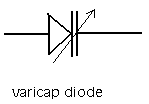
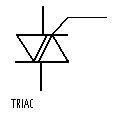
- thyristor, triac, triac, diac
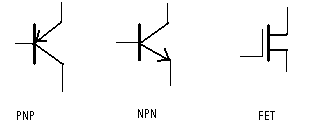
- transistoren: PNP, NPN, germanium transistor, silicium transistor, FET, MOSFET, UJT
2. andere
- Buizen: diode, kwikdampgelijkrichter, triode, tetrode, pentode, heptode, hexode
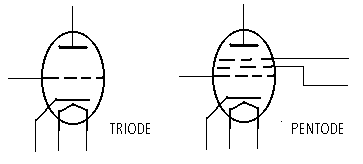
- dubbeldiode
- HF-diode
b. komplexe
1. analoge I.C.'s
- operationele versterkers
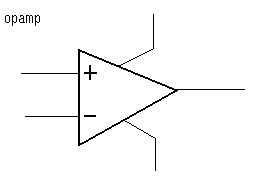
- oscillators
- V.C.O's
- P.L.L's
- Multipliers
2. digitale I.C.'s
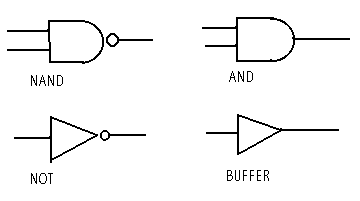
Logika chips
- Schuifregisters
- Flip-Flops
- RAM , ROM, EPROM , EEPROM, DRAM, PROM ...
- Microprocessors
- UARTS - USARTS
- DMA-chips
- PPI's en PIO's n m
- PAL's en GAL's
...
3. hybride I.C.'s
- comparators
- synthesizers
- BBDL's (analoge delay-lines)
- CCD's (videokamerachips)
- accelleratiesensoren, gassensoren, PIR-detektoren, HALL-sensoren
Alle komponenten worden getoond in de les. Tevens wordt uitgelegd hoe de komponenten te herkennen te zijn en hoe hun opschriften of kleurkodes moeten gelezen worden. Dit gedeelte kan nu eenmaal moeilijk in een syllabus worden opgenomen.De schemasymbolen kunnen ook vollediger (en grafisch verzorgder...) in andere publikaties getoond en weergevonden worden.
Kleurkodering van bepaalde elektronische onderdelen:
- elk kleur staat voor een bepaald cijfer. De betekenis van het cijfer hangt af van zijn positie.
De kleuren op de komponenten worden als cijfers gelezen volgens onderstaande tabel:
|
Zwart |
0 |
|
Bruin |
1 |
|
Rood |
2 |
|
Oranje |
3 |
|
Geel |
4 |
|
Groen |
5 |
|
Blauw |
6 |
|
Violet |
7 |
|
Grijs |
8 |
|
Wit |
9 |
Merk op -en dit is tevens een goed memotechnisch middel- dat deze kleurvolgorde grosso modo die is van de kleuren in de regenboog : Rood- oranje-geel-groen-indigo-violet (Roggbiv). Aan de onderkant van het spektrum werden zwart en bruin als 0 en 1 toegevoegd, en aan de bovenkant viel indigo wegens de slechte zichtbaarheid weg en werden grijs en wit als 8 en 9 toegevoegd.
De kleuren worden gelezen van links naar rechts. Wanneer op een weerstand vier kleurringen aanwezig zijn, worden ze gelezen alsvolgt:
1e ring = 1e digit
2e ring = 2e digit
3e ring = vermenigvuldigingsfaktor (aantal toe te voegen nullen)
4e ring = tolerantie ( de precisie - 5%, 10%, 20%)
Voor deze vierde ring , waarmee de foutmarge of de precizie van de komponent wordt aangegeven, worden meestal de kleuren:
|
Geen ring |
20% |
|
zilver |
10% |
|
Goud |
5% |
|
Rood |
2% |
|
bruin |
1% |
gebruikt.
Wanneer er geen vierde ring is, dan is de tolerantie 20%. Dergelijke weerstanden -met 20% precisie- komen echter vandaag nauwelijks nog voor. Wanneer de kleurkode echter bestaat uit 5 ringen, wordt ze gelezen alsvolgt:
|
1e ring |
1e digit |
|
2e ring |
2e digit |
|
3e ring |
3e digit |
|
4e ring |
vermenigvuldigingsfaktor |
|
5e ring |
Tolerantie in % |
vb. rood = 2%
bruin = 1%
Voor heel kleine weerstandswaarden is er met deze kodering een probleem. Het is immers niet zomaar mogelijk de decimale punt naar links op te schuiven. Daarom werden de kleuren zilver en goud als vermenigvuldigingsfaktor ingevoerd met volgende betekenis:
goud = decimale punt 1 plaats naar links
zilver= decimale punt 2 plaatsen naar links
Voorbeeld: Bruin Zwart Zilver Goud = 0,01 Ohm - 5%
Dezelfde kodering is ook voor kondensatoren van toepassing, met dien verstande dat de eenheid hier niet de Farad is, maar wel de pF!. Hier is een tolerantie van 20% echter heel gebruikelijk. Kondensatoren zijn immers moeilijker precies te maken dan weerstanden.
Voorbeeld: Geel Violet Groen = 47 00.000 pF - 20% = 4700nF = 4.7µF
Op heel erg kleine onderdelen (bvb. SMD's) is er vaak onvoldoende plaats op het lichaam van de komponent om er kleurkodes of volledige numerieke kodes op aan te brengen.
Vaak vinden we dan eerder aanduidingen zoals 473 wat op een weerstand aangebracht, betekent 47kOhm, maar, op een kondensator, 47nF of op een spoel 47mH. Op kondensatoren wordt een numerieke kode ook vaak aangebracht in de vorm 2n7, of n1, wat dan respektievelijk staat voor 2700pF en 100pF: de n (nano) staat op de plaats waar een decimale punt zich zou bevinden. Ook in elektronische schemas is dergelijke aanduiding heel gebruikelijk, ook voor weerstanden. (Dus 4k7, 8M2, ...).
De grondkleur van het onderdeel, heeft ook bijna steeds een betekenis. Zo slaat die bij Philips SMD weerstanden op de precisie: groen= 5%, blauw= 1%. Hierin worden echter geen universeel geldige kodes gebruikt. Men dient de data-boeken van de respektievelijke fabrikanten te raadplegen. Het probleem is echter vaak dat men deze niet steeds kent. Immers, wanneer op een onderdeel geen plek is voor het aanbrengen van een kode, laat staan dat er dan plaats zou zijn voor een merkaanduiding... Nameten is dan de enige oplossing.
Conditio sine qua non voor het juist toepassen van deze kodes is uiteraard het juist herkennen van de aard van het betreffende onderdeel! Weerstand, spoel of kondensator - bij geval van twijfel ben je aangewezen op een intelligent gebruik van een eenvoudige multimeter: wanneer het onderdeel geen weerstand vertoont is het bijna zeker een kondensator. Wanneer de gemeten weerstand veel kleiner is dan de door de kleurkode gesuggereerde waarde, hebben we te maken met een spoel! Bepaalde spoelen zijn op grond van de vorm quasi niet van weerstanden te onderscheiden.
Filedate: 920201/971011/011210
|
Naar decibell uitleg |
||
|
Terug naar inhoudstafel kursus: <Index Kursus> |
Naar homepage dr.Godfried-Willem RAES |
Naar volgende paragraaf : operationele versterker |