Dr.Godfried-Willem RAES

Kursus Experimentele Muziek: Boekdeel 1: Algoritmische Kompositie

Hogeschool Gent : Departement Muziek & Drama

1155:

FOURIER-ANALYZE

1. Spektrum Analyze

  Analyze kan worden beschouwd als de omgekeerde bewerking van syntheze. Toegepast op klank -golfvormen dus- laat analyze ons in principe toe om een willekeurige golfvorm (in het tijdsdomein) te ontbinden in elementaire samenstellende bestanddelen: een spektrum (in het frekwentiedomein).

Nu is het onjuist te denken dat dit slechts op een enkele wijze zou kunnen gebeuren. Immers, zoals we aantoonden in het hoofdstukje over syntheze, zijn er verschillende technieken mogelijk om eenzelfde golfvorm op te wekken. Omgekeerd kan worden aangetoond dat een onbeperkt aantal algoritmes kunnen worden opgesteld waarvoor geldt dat zij de samengestelde golfvorm adekwaat beschrijven.

Tot laat in de 19e eeuw -en retardaire muziektheoretici tot op de dag van vandaag geloven het nog- geloofde men dat golfvormen 'objektief' samengesteld waren uit 'atomaire' komponenten: zuivere sinusgolven in onderling wisselende sterkteverhoudingen. Bovendien meenden deze wetenschappelijk slecht of nauwelijks geschoolde muziekteoretici dat de samenstellende sinusgolven een eenvoudige boventoonsreeks vormden en dat elke klank was samengesteld uit een grondtoon en boventonen (gehele veelvouden van de grondtoon) die onderling op een voor elke klank typisch stelsel van amplitudeverhoudingen berusten. Deze opvatting is sedert lang geheel en totaal gefalsifieerd, niet alleen in haar toepasbaarheid op golfvormen in het algemeen, maar zelfs ook in haar toepasbaarheid op wat men 'muzikale' klanken pleegt te noemen.

Vooreerst staan de 'harmonischen' van de meeste akoestische klanken en geluiden zoals blijkt uit metingen- helemaal niet in zo'n eenvoudige getalverhoudingen tot elkaar (vb.: aangeslagen staven met een precieze toonhoogte hebben niet eens 2e en 3e harmonischen, lage pianosnaren hebben 'valse' oktaven, fluiten blazen over in intervallen die 'te klein' zijn...), en bovendien blijkt ook de aangenomen periodiciteit van de harmonischen een niet met de werkelijkheid overeenkomende assumptie. De oorzaak hiervan ligt in eerste plaats in het simpele feit dat akoestische trillingsbronnen noodzakelijkerwijze steeds minstens 3 vrijheidsgraden hebben en dus moeten worden gezien als meerdimensionele trillingssystemen...

Maar, zoals gezegd, kan een onbeperkt aantal algoritmes opgesteld worden om een gegeven golfvorm te beschrijven. Er zijn klaarblijkelijk geen 'elementaire deeltjes' behalve in het hoofd van wie ze nu eenmaal aan de werkelijkheid wil opdringen. De sinustonen waarvan de Fourier transformatie uitgaat blijken eerder 'arbitraire deeltjes' dan 'elementaire' deeltjes te zijn. De klassieke Fourieranalyze is dan ook slechts een van de analysemogelijkheden, al is het wel de meest bekende.

2. Fourier-analyze

 De techniek die voor dit soort spektraalanalyze het vaakst wordt gebruikt -en die deels voortkwam uit de atomaire opvatting van golfvormen- werd ontwikkeld door de Franse wiskundige Jean Baptiste Joseph Fourier (1768-1830).

Deze techniek die men de Fourier transformatie noemt stelt dat een willekeurige zich periodiek herhalende golfvorm (!) wiskundig kan worden ontbonden in een oneindig aantal sinusvormige komponenten waarvan men de onderlinge frekwentieverhouding, fazerelatie en amplitude kan berekenen. De omzetting van tijdsdomein naar frekwentiedomein is daarbij volstrekt omkeerbaar:

De fourier transformatie wordt gegeven door volgende formule:

 Het Fourier koppel in de meest algemene wiskundige zin bestaat uit:

¥

en: ¥

of, kortom: F (p) <= > F(x)

Wat we in 'muziektoepassingen' waarbij de de gekonjugeerde variabelen bijna steeds bestaan uit tijd en frekwentie formuleren als:

f(t) <=> F(f)

Fourier analyze behoort niet bepaald tot de eenvoudigste takken van de wiskunde, en een teoretisch-technische behandeling (laat staan het bewijs) ervan valt beslist buiten het bestek van deze syllabus. We geven bovenstaande integralen dan ook eerder ten titel van dokumentatie. Wie er zich de wiskundige achtergrond van wil eigen maken verwijzen we naar elk wiskunde, fyzika of signaaltheorie handboek voor het hoger onderwijs waarin integraalrekening en Fourier analyze telkens een onontwijkbaar en vast bestanddeel van de stof uitmaakt. Een goede wiskundige inleiding geeft: J.F.James "A student's guide to Fourier Transforms", Cambridge University Press,1995, ISBN 0 521 46829 9. Een meer exhaustieve behandeling vinden we in: Goldberg, R.R. 'Fourier Transforms' (Cambridge University Press, 1965). Een uitwerking speciaal gericht op toepassing in muzikale akoestiek vinden we in Philippe Guillaume 'Music and Acoustics' (ISTE, 2006)

Belangrijk om te onthouden zijn de mogelijkheden en beperkingen van de Fourier analyze als het gaat om signaalanalyze:

1.- zij geldt alleen voor signalen waarvan de periodiciteit wordt aangenomen.

vb. stel F(x).t = een periodieke funktie in de tijd.

2.- zij ontbindt deze signalen in periodieke (sinusoidale) komponenten

3.- zij is infinitistisch.

vb.: de funktie F(x).t wordt ontbonden in een oneindige som van de vorm:

A1.sin(w1.p1.t) + A2.sin(w2.p2.t) + A3.sin(w3.p3.t) + ....

waarin A1, A2,A3 ... = amplitudes van de spektrale komponenten

w1, w2, w3 ... = de cirkelfrekwenties van die komponenten

p1, p2, p3 ... = de fazehoeken (in radialen) van de komponenten

De algoritmes waarmee een Fourier analyze wordt uitgevoerd worden in de literatuur steeds aangeduid als FFT (Fast Fourier Transformations). Deze term slaat op het feit dat de gewone FT uiterst rekenintensief is, niet in het minst omdat zij de berekening veronderstelt van een ingewikkelde integraal voor een oneindig aantal spektrale komponenten, zodat wiskundigen en vooral technici middelen zochten om de berekening te versnellen (en te vereenvoudigen). Daarvoor werd uitgegaan van een aantal eigenschappen van periodieke verschijnselen, zoals hun symmetrie (op grond waarvan het aantal berekeningen kan worden gehalveerd) e.d.m. De algoritmiek voor de FFT is, eigenaardig genoeg, in beginsel ouder dan de Fourier analyze zelf want gaat terug op ideeen geformuleerd door Gauss in 1805. De praktische uitwerking ervan is echter merkwaardig recent en wordt algemeen toegeschreven aan Cooley en Turkey in de vroege jaren 60 van vorige eeuw. Door hun algoritmes werd het mogelijk een Fourier transformatie over 1024 punten 2 grootteordes sneller te berekenen dan via een normale DFT (een tot finitistische proporties teruggebrachte Fourier transformatie).

3. Diskrete Fourier Transformatie (DFT)

Zullen we in de kompositorische praktijk niet of nauwelijks nood hebben aan Fourier-analyzes van willekeurige kontinue golfvormen, dan kunnen we in de praktijk van de interaktieve kompositie en van de muzikale en klankanalyze (akoestiek) wel vaak gekonfronteerd worden met het vraagstuk van de bepaling van een of meer periodieke komponenten uit eindige reeksen samples van willekeurige golfvormen.

Voor de analytische behandeling van gesampelde signalen werden uitgaande van FFT-algoritmes, wiskundige behandelingstechnieken ontwikkeld die ons toelaten uit een gegeven aantal samples waarvan we verder volgende gegevens moeten kennen:

• 1.- de sampling rate
• 2.- de rezolutie
• 3.- aanwezige periodiciteit
• 4.- grenzen van het spektrum

de periodieke signaalkomponenten af te leiden.

De diskrete en finitistische basisformule voor deze operatie ziet eruit als:

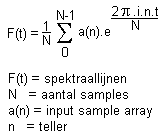
Merk op dat deze formule in feite veel gelijkenis vertoond met de eerder gegeven integraal. Bij de inverse bewerking moet slechts het teken van de komplekse exponent worden gewijzigd. De formule komt er dan uit te zien als:

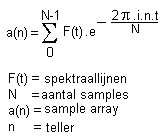
Deze techniek laat o.m. toe langs technisch-algoritmische weg redelijk precies de grondtoonhoogte te bepalen van een 'muzikale' toon, los van de spektrale samenstelling ervan.

Algoritmes voor Fourier analyze in deze beperkte (eindige) vorm staan in de literatuur bekend als DFT's (Discrete Fourier Transformations).

We hebben er zelf vaak gebruik van gemaakt, o.m. om uit het signaal afkomstig van de beweging van een 'dirigent' een muzikaal bazistempo af te leiden (cfr. 'A Book of Moves', 'Quadrada',' Gestrobo', 'Songbook' ). Bij die gelegenheid programmeerden we een DFT algoritme in Basic, dat beslist voor de analytisch ingestelde student lees- en verstaanbaar moet zijn.

Om de gang van zaken duidelijk te maken, hebben we in het hier volgende programma het DFT-algoritme ingebed in een programma dat eerst een golfvorm berekent uit bekende spektrale komponenten en dit als een sample-array aanbiedt aan het DFT-algoritme. Het programma laat prima toe de mogelijkheden en beperkingen van deze analyze techniek zelf uit te testen.

In mijn kompositie <Songbook> uit 1995 gebruikte ik deze techniek om het spektrum van een 'geste' (de globale vorm van een gebaar) af te beelden op de instellingen van een equaliser waarmee de klankkleur van een vokaal inputsignaal via beweging kon worden gestuurd.

Wie het zelf wil programmeren, bieden we hier een in een historisch basic (met regelnummers) geschreven programmaatje dat toelaat het gehele FFT algoritme te doorgronden.

• 1 'WAVEFORM SUMATION FOR FFT VERIFICATION *******
• 5 'This program generates 4 channels of sine wave data for
• 6 'specified frequency, amplitude and phase. This data is
• 7 'summed together to form an integrated wave form that will
• 8 'be used to test the accuracy of the FFT algorithm.
• 9 '-----------------------------------------------------------------
• 10 DIM FREQ(4),A(4),P(4): '- Frequency, Amplitude and phase
• 12 ' FREQUENCY(Hz) AMPLITUDE PHASE(Radians)
• 13 FREQ(0)=16: A(0)=10: P(0)=0:' Channel 0
• 14 FREQ(1)=9: A(1)=20: P(1)=0: ' Channel 1
• 15 FREQ(2)=8: A(2)=30: P(2)=0: ' Channel 2
• 16 FREQ(3)=2: A(3)=40: P(3)=0: ' Channel 3
• 17 WDW = 1!: ' Sample period in seconds
• 18 PT = 64: ' Number of sample points
• 19 MIN = 2: ' Minimum frequency to be evaluated (1 - 25)
• 20 MAX = 16: ' Maximum frequency to be evaluated (MIN - 25)
• 21 SM = 40: ' Offset to start of sample period
• 22 ' -----------------------------------------------------------------
• 23 PI = 3.14159
• 24 W = 2 * PI:' W (OMEGA) is 1 complete cycle in radians
• 25 DIM Y(5,150)
• 26 CLS
• 27 FOR F=0 TO 3
• 28 CLS
• 29 STP = W*FREQ(F)*WDW/PT
• 30 LOCATE 7,25 : PRINT "CALCULATING CHANNEL ";F;
• 31 FOR X = 0 TO 150
• 32 LOCATE 8,32 : PRINT X;
• 33 Y(F+1,X) = A(F)*COS(X*STP+P(F))
• 34 IF INKEY$ <> "" THEN END
• 35 NEXT X
• 36 NEXT F
• 37 GOSUB 900:' Display the wave forms
• 38 GOSUB 800:' Wait for user signal to continue
• 39 ' -----------------------------------------------------------------
• 40 ' ***** Prepare and calculate the DFT *****
• 41 DIM RAWDAT(300),FFT(300,3):' Initialize size of sample buffer
• 42 FOR X=0 TO PT
• 43 RAWDAT(X) = Y(0,X+SM):' Load the data points into the buffer
• 44 NEXT X
• 45 LOCATE 7,23 :PRINT "CALCULATING THE FFT ";MIN;"to";MAX
• 46 FOR HZ = MIN TO MAX
• 47 LOCATE 8,35 : PRINT HZ
• 48 REAL = 0
• 49 IMAG = 0
• 50 FOR X=0 TO PT-1
• 51 G = 2*PI*HZ*X/PT
• 52 REAL = REAL + RAWDAT(X)*COS(G)/PT
• 53 IMAG = IMAG - RAWDAT(X)*SIN(G)/PT
• 54 IF INKEY$ <> "" THEN END
• 55 NEXT X
• 56 FFT(HZ,0) = 2*SQR(IMAG*IMAG + REAL*REAL):' Power calculation
• 57 IF FFT(HZ,0) < 1 THEN FFT(HZ,0)=0
• 58 FFT(HZ,1) = ATN(IMAG/REAL):' Phase calculation
• 59 IF FFT(HZ,1) < 1 THEN FFT(HZ,1)=0
• 60 FFT(HZ,2) = REAL:' Real component
• 61 IF FFT(HZ,2) < 1 THEN FFT(HZ,2)=0
• 62 FFT(HZ,3) = IMAG:' Imaginary component
• 63 IF FFT(HZ,3) < 1 THEN FFT(HZ,3)=0
• 64 PRINT " "
• 65 NEXT HZ
• 100 CLS:PRINT "Hz","Amplitude","Phase","Real","Imaginary"
• 101 FOR HZ=0 TO 21
• 102 PRINT HZ,FFT(HZ,0),FFT(HZ,1),FFT(HZ,2),FFT(HZ,3)
• 103 NEXT HZ
• 104 LOCATE 25,30 : PRINT "Escape to DOS";
• 105 GOSUB 800:' Wait for user signal to continue
• 106 ' -----------------------------------------------------------------
• 107 GOSUB 900:' *** Display the wave forms ***
• 108 FOR X = 0 TO PT:' *** Now display the FFT ***
• 109 XX = (SM+X)*3+30 110 YY = 30 - FFT(X,0)/2
• 111 LINE (XX,30) - (XX,YY)
• 112 NEXT X 113 GOSUB 800:' Wait for user signal to continue
• 114 GOTO 100
• 115 END
• 116 ' -----------------------------------------------------------------
• 117 ' -----------------------------------------------------------------
• 800 K$=INKEY$:IF K$ = "" THEN 800
• 801 SCREEN 0
• 802 IF K$=CHR$(27) THEN END
• 803 RETURN
• 804 ' -----------------------------------------------------------------
• 805 ' Plot the sine waves and the integrated wave
• 900 SCREEN 2
• 901 FOR X=0 TO 150
• 902 Y(0,X)=Y(1,X)+Y(2,X)+Y(3,X)+Y(4,X)
• 903 XX = X*3+30
• 904 FOR L=0 TO 4
• 905 YY = 30*(L+1)+Y(L,X)/4
• 906 PSET (XX,YY)
• 907 NEXT L
• 908 NEXT X
• 909 ' **** Display the sampling defined for FFT ****
• 910 X = SM*3+30
• 911 LINE (X,0) - (X,199)
• 912 X = X + PT*3
• 913 LINE (X,0) - (X,199)
• 914 RETURN

4. DFT-Basic programma/procedure

zie nieuwe versies beschikbaar in de source code voor de GMT library (loopt onder alle Windows versies). Konsulteer de manual voor de gebruiksaanwijzing. De source is geschreven in Power Basic voor hun onvolprezen Windows compiler (2013).

5. Algemeen FFT programma voor Power Basic 3.2

Een veel verder en algemener uitgewerkt voorbeeld voor veralgemeende fourier-analyse schreef ik voor de studenten in 1997. Het programma vormt tevens een goed voorbeeld voor programmeren in de Power Basic omgeving onder DOS.

De kern van het Fourier-analyze algoritme geef ik via internet :

URL: ../fft/fft.html 

De executable: fft.exe vormt tevens een mooi voorbeeld voor FFT's en loopt in een volledig DOS scherm op alle PC's voorzien van een koprocessor. (Sedert de Pentium is deze voorwaarde altijd voldaan trouwens).

../fft/fft.exe

De studenten wordt sterk aanbevolen met het programma wat te experimenteren. Het is eenvoudig aan te passen voor gebruik met zelf gedefinieerde golfvormen, voor externe sample-data files en voor abstrakte wiskundige analyse. Zowel de volledige bronkode als de gekompileerde versie staan ter beschikking. Er zijn heel wat grafische hulpmiddelen opgenomen in de kode. Ook uit de bestudering van die kode valt een en ander te leren.

6. Spektrum naar wave en wave naar spektrum transformatie: zie 1157.html

7. Zoom FFT

Vaak zijn we helemaal niet geinteresseerd in het gehele spektrum van een signaal, maar slechts in een welbepaald stukje daarvan. Bijvoorbeeld wanneer we de toonhoogteafwijking van de harmonischen van pianosnaren willen meten en berekenen,of, wanneer we geinteresseerd zijn in de door het Doppler effekt veroorzaakte verschuiving van de waargenomen toonhoogte versus de uitgezonden toonhoogte bij bewegende waarnemers of geluidsbronnen (cfr. radar en sonar). In dergelijke gevallen kunnen we de komplexiteit van de berekeningen enorm reduceren door de analyse slechts uit te voeren op het gedeelte van het spektrum (de frekwentieband) die ons interesseert. Er bestaan erg veel verschillende technieken om dit te bereiken. Een van onze eigen favorieten bestaat erin het te onderzoeken signaal te vermenigvuldigen met een sinussignaal overeenkomstig de centrale frekwentie van de band die ons interesseert. Hierdoor verschuiven we die band naar een frekwentiegebied vanaf nul Hz. (In de radiotechniek staat dit bekend als FM demodulatie). Vervolgens laten we dit signaal een scherp low pass filter doorlopen en tot slot kunnen we het , al dan niet na downsampling, een FFT laten ondergaan. Deze techniek kan gemakkelijk in real time worden toegepast op gangbare komputers. Zij vormt trouwens de kern van het door ons ontwikkelde onzichtbaar instrument, zowel in radar als in sonar techniek.

8. Joint Time Frequency Analysis (JTFA)

De meeste in de ons omringende wereld voorkomende signalen en geluiden veranderen wel degelijk in funktie van de tijd... Deze eigenschap maakt hen in principe bij voorbaat ongeschikt voor een Fourier analyse. Daarom zijn wiskundigen, wetenschapsmensen en technici nog steeds erg in de weer met het zoeken naar een apparaat om dergelijke signalen snel en akkuraat te analyzeren. Bij JTFA worden Fourier transforms gebruikt over een klein in de tijd voortschuivend venster op het signaal. De frekwentieveranderingen in het spektrum zijn het resultaat van de analyze.

9. Super Resolution Spectral Analysis (SRSA)

Een van de invalshoeken bij het probleem van de analyse van niet periodieke signalen, bestaat erin het signaal te vergelijken met een eveneens tijd-veranderlijk model. De mate van overeenkomst met het model kan met een korrelatiefunktie worden berekend. Dergelijke analyse methodes gaan evenwel uit van een zekere a priori kennis van de te verwachten signalen en de erin potentieel voorkomende spektrale komponenten en kunnen dan ook niet op algemene geldigheid aanspraak maken.

Te zien in het Gentse Museum van de Wetenschap (Ugent):

Klankanalysator van Koenig (ca. 1870). Bij dit instrument is elk van de ingebouwde Helmholtz resonatoren verbonden met een gasbrander. Wanneer bij het produceren van geluid de resonatoren meetrillen bij hun eigenfrequentie, dan wordt deze trilling overgezet op de vlam waardoor deze gaat flikkeren. Op deze manier kan men achterhalen welke frequenties vervat zijn in een bepaald geluid.

Ook mechanische spektrum analysers werden sedert de 19e eeuw gebouwd. Ze bestaan uit een reeks slingers, elk met een eigen frekwentie die aangedreven worden door een enkele as die een periodieke beweging maakt. Aan de hand van de resonanties van de slingers kan worden bepaald wat de spektrale samenstelling van de periodieke beweging is.

De toestellen die vroeger werden gebruikt om de netfrekwentie te meten, waren opgebouwd uit een reeks stalen tongen gestemd in frakties van een Hz in een bereik van bvb. 45 tot 55Hz die geplaatst werden in een elektomagnetisch veld opgewekt door een spoel aangesloten op de netspanning. In feite waren het kleine smalbandige spektrum analysers.

Filedate: 951003/ last update: 2013-04-29