Prof.Dr.Godfried-Willem RAES

<GMT> Reference Manual: Math library functions and procedures

This section covers the reference and user manual for all functions contained in the source code module g_math.inc. The corresponding declaration file is g_math.bi.

The compiled library is contained in g_lib.dll and the declaration file with all exported functions in g_lib.bi.

If the file g_lib.bas is compiled, the compilation of this source code is always included in the resulting DLL. (g_lib.dll). Routine math procedures and makros are not explaned here (refer to any good textbook on math) , only more specific functions and procedures are fully documented.

Changes since version 5.2: functions and procedures that are completely independent of the GMT context are now compiled to a specific general purpose DLL: g_indep.dll. The declarations for all exported functions can be found in the file g_indep.bi.

Changes since version 5.9: many math functions added. New general Triangle-solver function.

Procedures for the conversion from polar to cartesian complex numbers and vice versa.

SUB P2C (P AS Polar, C AS Complex)

converts a complex number expressed in polar coordinates to its cartesian equivalent. Refer to the type declaration file to see the structure of the arguments.

SUB C2P (C AS Complex, P AS Polar)

converts a complex number expressed in cartesian coordinates into its polar equivalent. Refer to the type declaration file to see the structure of the arguments.

Conversion from angles expressed in Radians to degrees and vice versa:

FUNCTION Rad2Deg# (rad#)
FUNCTION Deg2Rad# (degrees#)

Polar coordinate algebra:
SUB MulPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)

Multiplies two complex numbers given in polar coordinates. Refer to the type declaration file to see the structure of the arguments.

SUB DivPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)

Divides two complex numbers given in polar coordinates. Refer to the type declaration file to see the structure of the arguments.

SUB AddPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)

Adds two complex numbers given in polar coordinates.Refer to the type declaration file to see the structure of the arguments.

SUB SubPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)

Subtracks two complex numbers given in polar coordinates.Refer to the type declaration file to see the structure of the arguments.

SUB InvPol (G1 AS Polar, Gr AS Polar)
SUB ConPol (G1 AS Polar, Gr AS Polar)
SUB ParPol (G1 AS Polar, G2 AS Polar, Gr AS Polar)

Cartesian complex number algebra:
SUB MulCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)

Multiplication of complex numbers

SUB DivCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)

Division of complex numbers

SUB AddCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)

Addition of complex numbers

SUB SubCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)

Substraction of complex numbers

SUB InvCom (G1 AS Complex, Gr AS Complex)

Inversion of a complex number.

SUB ConCom (G1 AS Complex, Gr AS Complex)
SUB ParCom (G1 AS Complex, G2 AS Complex, Gr AS Complex)
FUNCTION MagCom# (G1 AS Complex)

Returns the magnitude of a complex number

FUNCTION AngCom# (G1 AS Complex)

Returns the phase angle of a complex number

Arithmetic functions

FUNCTION IsPrime (BYVAL n AS DWORD) AS DWORD

returns %True if the number passed is a prime number, else returns %False

FUNCTION NextPrime (BYVAL n AS DWORD) AS DWORD

returns the next prime number greater than the number passed

FUNCTION PrevPrime (BYVAL n AS DWORD) AS DWORD

returns the first primenumber smaller than the number passed

Electronics functions and procedures: (indexed o.k.)

FUNCTION OmegF# (f#)

A macro returning 2 * Pi * f#.

SUB XcCar (C#, f#, G AS Complex)

A procedure returning the capacitive reactance of a capacitor of value C# at a frequency f#. The value is returned as a complex number.

SUB XcPol (C#, f#, G AS Polar)

A procedure returning the capacitive reactance of a capacitor of value C# at a frequency f#. The value is returned as a complex number in polar coordinates.

SUB XlCar (L#, f#, G AS Complex)

A procedure returning the inductive reactance of a coil of value L# at a frequency f#. The value is returned as a complex number.

SUB XlPol (L#, f#, G AS Polar)

A procedure returning the inductive reactance of a coil of value L# at a frequency f#. The value is returned as a complex number in polar coordinates.

Second order functions (quadratic) and triangular numbers

SUB SolveEqDeg2 (a!, b!, c!, root AS Roots)

FUNCTION Lemniskaat (hoek AS SINGLE) AS SINGLE

Macro returning the infamous 'infinity' sign as a periodic function.

SUB Oxalis (hoek AS SINGLE, G AS Complex)

Macro returning a double Lemnisate function in 4 quadrants.

FUNCTION TriangleNumber! (i AS SINGLE)
FUNCTION TriangleNumberLimit (x AS SINGLE) AS SINGLE
FUNCTION BinomialComb (n AS WORD, k AS WORD) AS DWORD

FUNCTION Kummer (x AS SINGLE, y AS SINGLE, z AS SINGLE, mu AS SINGLE) AS SINGLE

This function describes a family of surfaces discovered by Ernst Eduard Kummer in 1864. There is a family of Kummer surfaces admitting the symmetry of the tetrahedron. This function returns exactly that family.
The mu^2 parameter should be choosen away from 1/3, 1 and 3.
'With mu = 13/10 you get the picture as on the cover of Linux 6.1 (suse build).

ref.: http://www-groups.dcs.st-and.ac.uk/~history/mathematicians/kummer.html

LOCAL lambda AS SINGLE
LOCAL p AS SINGLE
LOCAL q AS SINGLE
LOCAL r AS SINGLE
LOCAL s AS SINGLE
lambda = ((3 * (mu^2)) - 1 ) / (3- (mu^2))
p = 1 - z - (SQR(2) * x)
q = 1 - z + (SQR(2) * x)
r = 1 + z - (SQR(2) * y)
s = 1 + z + (SQR(2) * y)
FUNCTION = (((x^2) + (y^2) + (z^2) + (mu^2))^2) - (lambda * p * q * r * s)

Goniometric functions:

FUNCTION Sinc (SINGLE) AS SINGLE

This is an implementation of the (sin(x))/x function. The angle parameter has to be passed in radians.

FUNCTION Cosc (SINGLE) AS SINGLE

This is a macro implementing the function '(cos(x)/ x) . Angles have to be passed in radians.

FUNCTION ChargeCap (RC AS SINGLE, t AS SINGLE) AS SINGLE
FUNCTION DisChargeCap (RC AS SINGLE, t AS SINGLE) AS SINGLE

FUNCTION ArcSin (SINGLE) AS SINGLE

FUNCTION ArcCos (SINGLE) AS SINGLE

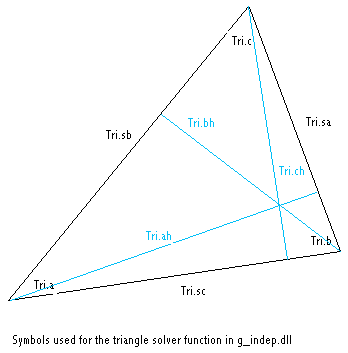
FUNCTION TriangleMath (T as Triangletype) AS DWORD

This function solves arbitrary triangles, given 3 elements, if possible. Look into the declaration of the triangle (cfr. g_type.bi) structure for documentation. The figure below can be used as a point of reference to understand the parameters of the function:

FUNCTION Lim2Pow2 (value AS DWORD) AS DWORD

returns the number smaller or equal than the value passed, that is an integer power of 2. The function is used to optimize Fourier transforms.

FUNCTION NrSamp2Samptim (BYVAL NrSamp AS BYTE, BYVAL Sr AS SINGLE) AS WORD
FUNCTION SampTim2NrSamp (BYVAL SampTim AS WORD, BYVAL Sr AS SINGLE) AS BYTE
FUNCTION dBV2val (dB AS SINGLE) AS WORD
FUNCTION val2dBV (value AS INTEGER) AS SINGLE

Periodic functions (generators):
FUNCTION Triangle (hoek AS SINGLE) AS SINGLE
FUNCTION Saw (hoek AS SINGLE, dc AS SINGLE) AS SINGLE
FUNCTION Square (hoek AS SINGLE, dc AS SINGLE) AS INTEGER

Audio signal analysis functions and procedures:

These functions are used for transforms, wavelets, convolutions and correlations:
SUB DFT (Samp!(), Spectrum!())

SUB InvDFT (Spectrum!(), Samp!())

FUNCTION Qsine (BYVAL samplingrate AS DWORD, BYVAL noot AS SINGLE, BYREF WavLet() AS SINGLE) AS DWORD

returns the data for 1/4th of a period of sinewave at samplingrate %CD_SR for the frequency corresponding to the midi note passed. The resulting lookuptable is returned in WavLet(). The Wavlet() array is redimensioned in the procedure.

SUB PrepareWaveletTables (BYREF WaveLets AS WaveLetData)

Fills and prepares an interval lookuptable containing 1/4th periods of sinewaves foor all valid midi note frequencies. It is an nternal procedure to generate a lookup with quart sines for the noterange 36-96 whereby the samplingrate must be 44100S/s. The limit notes 36 to 96 (5 octaves) is fixed by the type declaration. The lookups are used for polyphonic pitch recognition in real time audio.

FUNCTION CorrelateNoteToWave (BYVAL noot AS SINGLE, Sp() AS SINGLE) AS SINGLE

Call this function in a loop for notes, after obtaining a normalized (and lowpass- filtered, if required) period from the waveform.
The wave in Sp() must be normalised with values ranging from -1 to +1. The result of the function is normalised 0-1

FUNCTION IsolateSinglePeriod (BYVAL Track AS LONG, Sp() AS SINGLE, BYVAL param AS DWORD) AS SINGLE

This function returns the period for the most recent full wavecycle found in the audiotrack passed in Track, expressed in seconds. If no period could be found, the function returns %false. The sample data for the complete period will be returned in Sw(). The function does not perform a low pass filtering on the input, so it is up to the user to first pass the data through a suitable lowpass filter stage.

FUNCTION IsolateSingleWave (BYREF Sp() AS SINGLE ,BYREF Sw() AS SINGLE) AS SINGLE

This function returns the period for the most recent full wavecycle found in the normalized spectrum passed in Sp(), expressed in seconds. If no period could be found, the function returns %false. The sample data for the complete period will be returned in Sw(). The function does not perform a low pass filtering on the input, so it is up to the user to first pass the data through a suitable lowpass filter stage.

FUNCTION IsolateSingleZeroCrossWave (BYREF Sp() AS SINGLE ,BYREF Sw() AS SINGLE, BYVAL noise AS SINGLE) AS SINGLE

SUB GetWaveProperties (BYREF Sp() AS SINGLE, BYREF WavProp AS WaveProperties)

The array passed in Sp() should contain a chunk of audio information (44.1kS/s) in bipolar normalized format. The function will attempt to isolate a full period from the tail of this array and fill a WaveProperties structure with the result of the analysis of this single period. It is advisable to apply a lowpass filter (cfr. LowPass(Sp(),faktor) ) on Sp() prior to calling this function. Obviously the function will only return meaningfull information if the input contains periodic information. The Waveproperties structure is prototyped as:

TYPE WaveProperties DWORD
freq AS SINGLE ' frequency as derived from the period duration
pospeak AS SINGLE ' peak positive value
negpeak AS SINGLE ' peak negative value
pos AS SINGLE ' integral of positive half of the period
neg AS SINGLE ' integral of negative half of the period
correlation AS SINGLE ' normalized correlation with a sine wave of the same frequency
amplitude AS SINGLE ' calculated as a true integral of the wavesurface. Normalized to 0-1
symmetry AS SINGLE ' difference between positive and negative surface (-1 to + 1)
note AS LONG ' nearest midi note equivalent
velo AS LONG ' midi velocity equivalent, derived from amplitude
END TYPE

On return from the procedure either an empty structure will be obtained , if the procedure could not find suitable data in the input, or else a complete filled out structure. The algorithm used for isolating a single period is identical to the algorithm used in our IsolateSingleWave procedure.

SUB LowPass (BYREF Sp() AS SINGLE, BYVAL faktor AS SINGLE)

Sp() is the array containing the samples to be filtered. The filter operates in-place, i.e. it replaces the contents of Sp() with its output. The faktor parameter is the division factor for the sampling rate in use. This determines the -3dB cutoff frequency.
So, if we want a cut of frequency of 2205Hz and the initial sampling rate is %CD_SR, we should set faktor to 20.

Filedate: 00-04-27

Last update: 2004-10-30